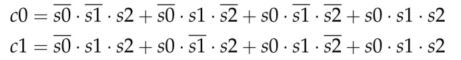Week 2 Data types, operators, combinational logic
Relevant Digital Logic lecture videos:
Intro to number systems
Number conversion
Fractional number conversion
2's complement
The Youtube lecture playlist of Digital Logic (CE241)
1. Please review the number systems
Number conversions among binary, decimal, octal, and Hexidecimal
1's and 2's complement for negative numbers
2. Fixed-Point Representation
Binary number to be processed in a digital system may have a fractional
part. There are two methods to represent a binary number with integer
and fractional parts. These are fixed-and floating-point
representations.
Please print and read through this PDF file for this section on the textbook.
Example 1: (unsigned, UQ16.16)
14.125(10) = 1110.001 (2) = 0000 0000 0000 1110.0010 0000 0000 0000
= 000E.2000
= 000E.2000 (UQ16.16)
Example 2: (signed, UQ15)
-14.125(10) = 1000 0000 0000 1110 (2) = 800E (losing the fractional part)
Example 3: (signed, UQ15.16)
-14.125(10) = 1000 0000 0000 1110.0010 0000 0000 0000 (2) = 800E.2000
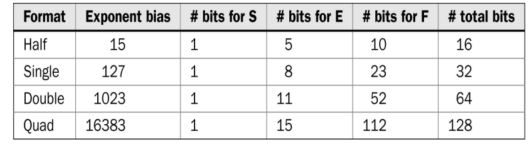
3. Floating-Point Representation
In floating-point representation, a binary number with fractional part
will be shown as N = (−1)^S × 2^E × F. Here, S stands for the sign bit,
E represents the exponent value, and F stands for the fractional part.
Then, floating-point number N is kept in memory as X = SEF.
Example 1:
14.125 in half precision/format:
14.125 (10) = 1110.001 = 1.110001 x 2^(3)
=> S = 0
=> E = 15 + 3 = 18 = 10010
=> F = 110001 0000
=> X = SEF = 0 10010 110001 0000 = 0100 1011 0001 0000 = 4B10(16)
Example 2:
-14.125 in half precision/format:
X = SEF = 1 10010 110001 0000 = 1100 1011 0001 0000 = CB10(16)
Example 3:
0.125 in Half precision/format:
0.125 (10) = 0.001 (2) = 1.0 x 2^(-3)
=> S = 0
=> E = 15-3 = 12 = 01100 (must be 5 bits)
=> F = 0000000000 (must be 10 bits)
=> X = SEF = 0 01100 0000000000 = 0011 0000 0000 0000 = 3 0 0 0 (16)
You can check the results on this online conversion tool:
https://evanw.github.io/float-toy/
Verified:

Example 4:
3.141 in half precision/format:
Use an online converter to conver 3.141 to its binary form:
https://www.rapidtables.com/convert/number/decimal-to-binary.html
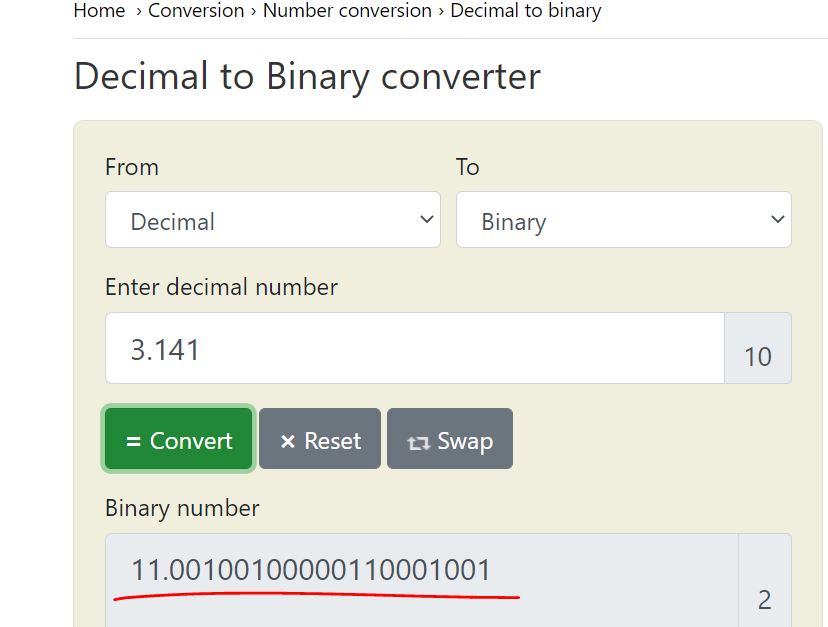
which is 1.1001 0010 0000 1100 0100 1 x 2^1
=> S = 0
=> E = 15 + 1 = 16 = 10000
=> F = 1001 0010 0000 1100 0100 1, only keep 10 bits - 1001 0010 00
=> X = SEF = 0 10000 1001 0010 00 = 0100 0010 0100 1000 = 4248
The IEEE 754 standard for floating point representation
4. Fixed point addition
Adding two binary numbers represented by the same unsigned fixedpoint format (straightforward)
Two binary numbers represented in UQ8.4 format as 0000 1110 0010 and 0010 0111 0110. The sum will be 0011 0101 1000
The first and second numbers are 14.125 and 39.375 in decimal form with
the sum 53.5. The sum obtained in UQ8.4 format is also the same as this
number is in binary form.
If the numbers are signed and the two fixed point numbers have different signs, it belongs to the subtraction category.
If they have the same sign, the sign bit shouldn't be taken into account in the addition operation.
5. Floating point addition
A binary number is represented as N = (−1)^S × 2^E × F in floating-point form. Moreover, the number is saved as X = SEF.
When addting to numbers, the exponent value E should be the same. For example:
14.125 + 39.375 = 1110.001 + 100111.011 = 0 10010 110001 0000 + 0 10100
00111011 00, however, these shouldn't be added together. The exponent
value must be equated first before the addition:
1110.001 = 1.110001 x 2^3
100111.011 = 100.111011 x 2^3
Add them together:
(1.110001 + 100.111011) x 2^3 = 110.101100 x 2^3 = 1.10101100 x 2^5
Fianlly, X = 0 10100 10101100 00
6. Fixed point subtraction
Example 1: (UQ8.4) (use 2's complement for negative numbers)
39.375 - 14.125 = 00100111.0110 - 00001110.0010 = 00100111.0110 + (-00001110.0010)
Note that -00001110.0010 = -00001110 + (-.0010) = 11110010 + 11111111.1110 = 11110001.1110 (adding 1's in front of a 2's complement negative number will not change the value).
so, 39.375 - 14.125 = 00100111.0110 + 11110001.1110 = 1 00011001.0100 = 00011001.0100
Here, we discard the carry '1' becuase it is not an overflow, it is an
error due to the use of 2's complement. If it is an overflow, that
carry should be used as the MSB. More explanation follow:
-----------------------
The textbook says 'overflow' occurs. Keep in mind that in digital
domain, this is not called 'overflow', it is called carry out. The
rules of overflow is defined as follows. Just remember that, overflow
only occurs when P + P = N, or N + N = P.
The rules for detecting overflow in a two's complement sum are simple:
If the sum of two positive numbers yields a negative result, the sum
has overflowed. If the sum of two negative numbers yields a positive
result, the sum has overflowed. Otherwise, the sum has not overflowed.
It is important to note the overflow and carry out can each occur
without the other. In unsigned numbers, carry out is equivalent to
overflow. In two's complement, carry out tells you nothing about
overflow. The reason for the rules is that overflow in two's complement
occurs, not when a bit is carried out out of the left column, but when
one is carried into it. That is, when there is a carry into the sign.
The rules detect this error by examining the sign of the result. A
negative and positive added together cannot overflow, because the sum
is between the addends. Since both of the addends fit within the
allowable range of numbers, and their sum is between them, it must fit
as well.
-----------------------
Example 2: (UQ8.4) (use 2's complement for negative numbers)
0000 1110.0010 - 0010 0111.0110 = 0000 1110 0010 + (- 0010 0111.0110) = 0000 1110.0010 + 11011001 + (-0.0110) = 0000 1110.0010 + 11011001 + (11111111.1010) = 11100110.1100
7. Floating point subtraction
Example 1: (half precision)
39.375 - 14.125
For E: 100.111011 x 2^3 - 1.110001 x 2^3 = 011.001010 x 2^3 = 1.1001010 x 2^4, therfore, E = 10011
S = 0
F = 1001010 000
So X = 0 10011 1001010 000 = 4E50
Example 2: 14.125 - 39.375
14.125 - 39.375 = -(39.375 - 14.125), then repeat the operation procedure above.
The result would be -(0 10011 1001010 000) = 1 10011 1001010 000. Keep in mind that there is no 2's complement in floating point numbers.
A quick qustion here: why you don't want to convert 14.125 - 39.375 into 14.125 + (-39.375) for the operation?
8. Fixed point multiplication
Example 1:
14.125 x 39.375 = 0000 1110 0010 x 0010 0111 0110 = 11100010 x 2^-4 x
1001110110 x 2^-4 = 11100010 x 1001110110 x 2^-8 =
100010110000101100×2^−8 = 1000101100.00101100 = 00101100.0010 (UQ8.4) (The result is incorrect becuase there are not enough bits to hold the correct value)
Overflow occurs so a larger format should be used.
9. Floating point multiplication
You must convert the floating point numbers back to its binary form and
then run the multiplication. The final result should be converted back
to the floating point format.
10. Division
For fixed point number divisions, there is no difference compared to regular binary number divisions
For floating point number divisions, similar to the multiplication
operation, you must convert it to its binary form first and then run
the operation.
10. ASCII Code
We do not only process numbers in digital systems. For some
applications, we may need to handle characters and symbols as well. We
know that everything in a digital system is represented in binary form.
Therefore, characters and symbols should also be represented as such.
One way of representing characters and symbols in binary form is using
the ASCII code. ASCII stands for the American Standard Code for
Information Interchange.
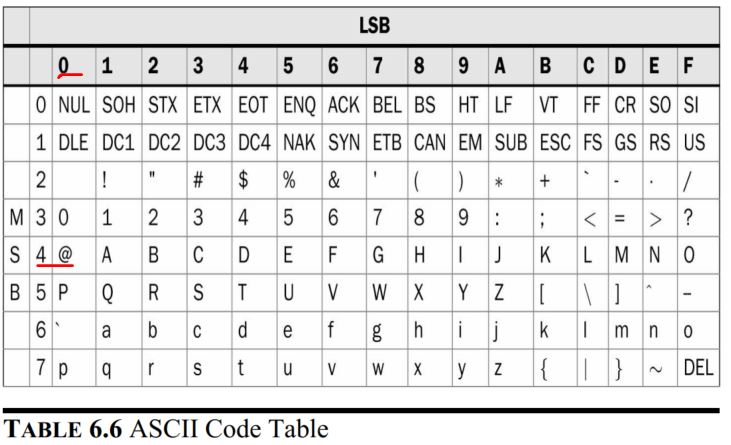
To represent a specific character (or symbol), its corresponding code
should be given. Let’s assume that we would like to represent the @
symbol. Using the following table, the corresponding ASCII code in
hexadecimal form will be 40.
11. Net/Data types in Verilog
Net:
wire: a wire connecting two elements
Variable:
reg: one-bit data (a DFF)
integer: 32-bit long
Data values:
0: logic 0
1: logic 1
x: don't care
z: high impedance (open circuit or disconnected)
Constants and parameters:
examples:
1'b0: a 1-bit binary number 0
2'b10: a 2-bit binary number 10
4'b10: the binary number 0010
6'o75: 6-bit octal number (6-bit means 6 binary bits)
8'hCA: 8-bit hex number CA
8'd251: the decimal number 251 is represented by 8 bits.
Vectors:
[N-1:0] prefix: there are N net variable entries packed as a vector.
MSB and LSB are the N-1th and the zeroth entries respectively.
example: wire [7:0] A. In this declaration, A is a wire data type with
8 bits. If you use 'A', it has all the 8 bits; if you use A[5:0] it
only take the lower 6 bits.
example: wire [0:7] A. MSB becomes A[0], LSB becomes A[7].
A quick simulation example from the textbook:
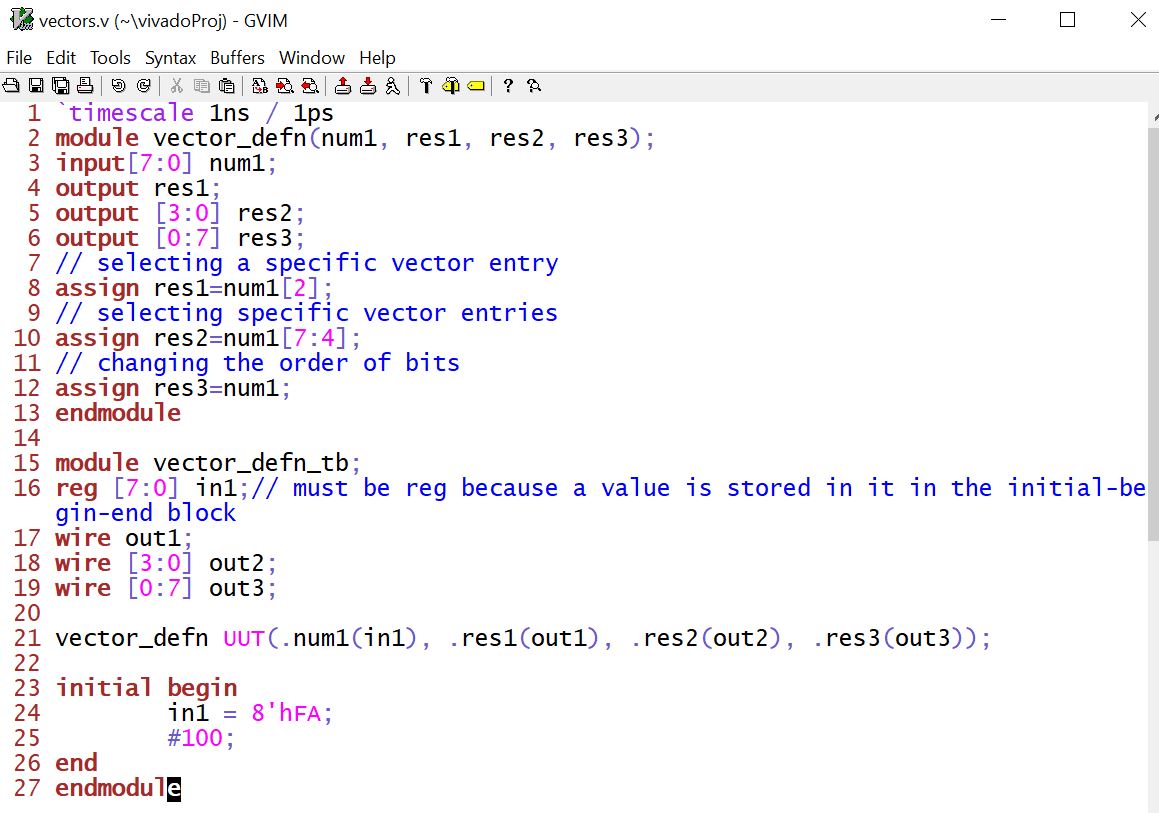
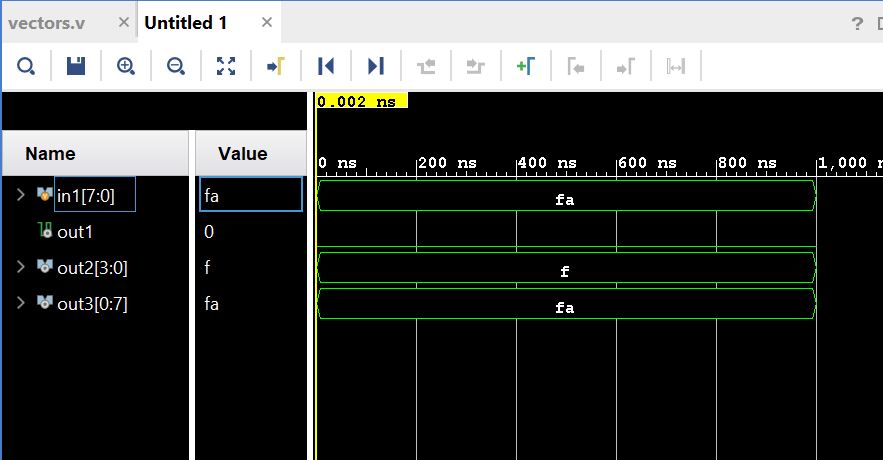
* Logic gates
NOT, OR, AND, XOR logic in Verilog:

12. Boolean algebra in Verilog


13. LUTs (look-up tables)
Combinational circuits are implemented by LUTs in an FPGA. A generic
LUT is composed of a multiplexer and memory elements in its basic form.
We can take the NOT gate as an example of one-input combinational
circuit.
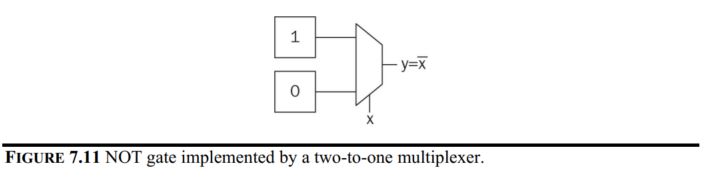
For two-input combinational circuits, the truth table and the LUT look like this:
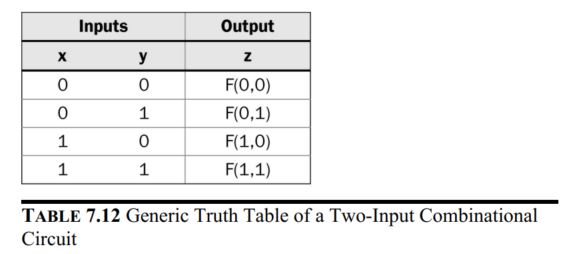
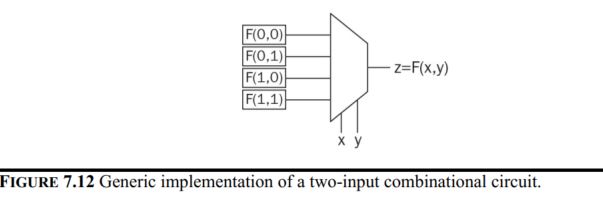
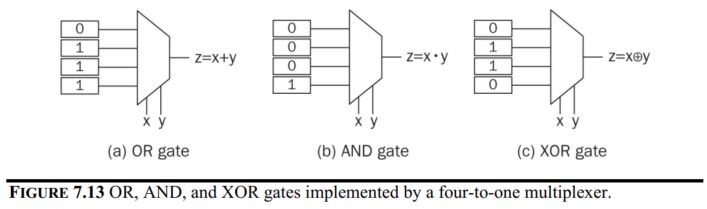
Examples of the standard gates:
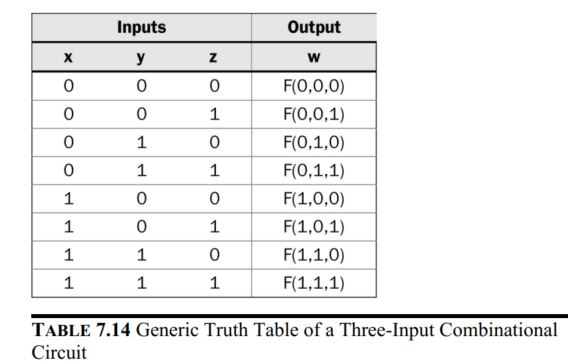
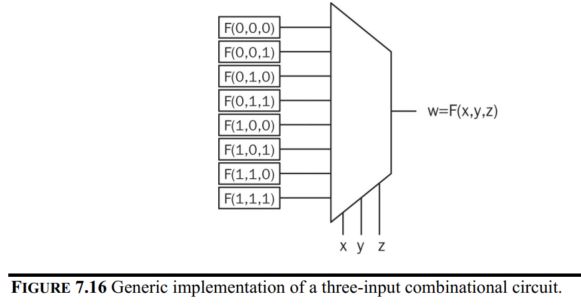
For three-input combinational circuits, the truth table and the LUT look like this:
14. Example of combinational logic design
14.1 A home alarm system
- Four inputs from output of 4 sensors connected to 3 windows and 1 door at home.
- One input as a switch to activate the entire system.
- One output to turn on the alarm.
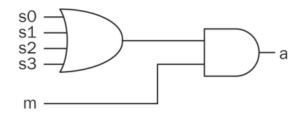
The Verilog description of the alarm system.

Implement it on the Basys3 board:
Create a new '.v' file from the command line.

Once the gvim window is opened, type the homeAlarm module into it.
Also, open a new window using ':vert new homeAlarm_top.v' command.
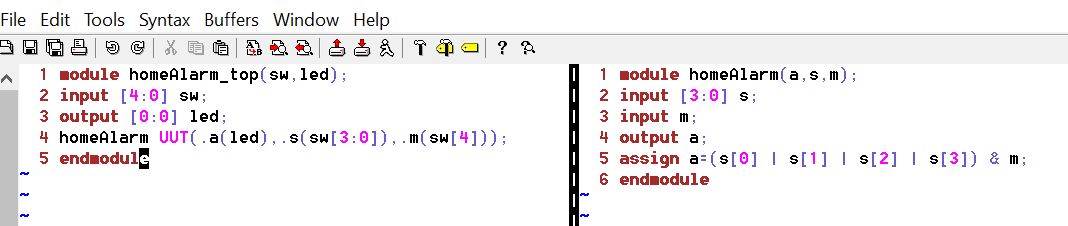
In Vivado, disable the previous sources buy right-clicking the file and
select 'Disable File'. Also, add the two source files you just created.
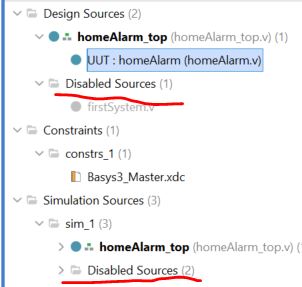
Add the constraint file 'Basys3_Master.xdc' using the '+' button. (you can download it from here. Unzip it before adding it to Vivado).
Run the Synthesis, Implementation, and Bitstream Generation respetfully.
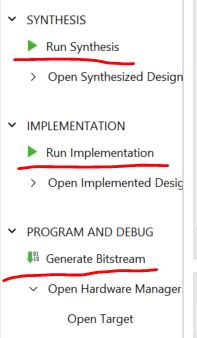
Then click 'Open Hardware Manager' to open a new target if it is the
first time to use the Basys3 Board on your computer. Otherwise, open a
recent target.

Results:

14.2 Digital safe system
There is a predefined password stored in the system. Every bit of the input must match the stored bits.
Use XOR to check if every bit matches. If it does, XOR gate outputs
0's. Invert the 0's to get 1's which are used as the input to one
4-input AND gate.
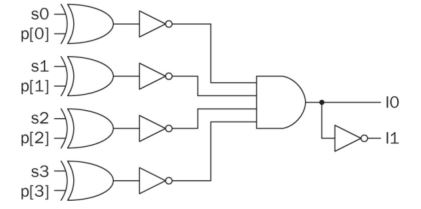
The Verilog script:

Implement this on the Basys3 Board:

When the input is 0101 (MSB - LSB), led[0] lights up, otherwise, led[1] lights up.

14.3 Car parking occupied spots counting system
S0, S1, and S2 are the three spots on the parking lot. Output C1C0 is
the 2-bit binary number that represents the count of the occupied
spots.
The truth table of the logic:
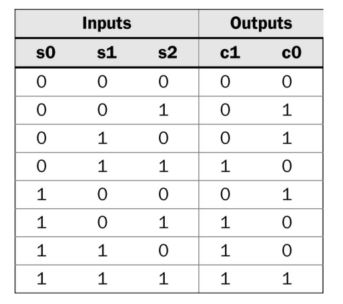
From the truth table, the following logic expression was created:
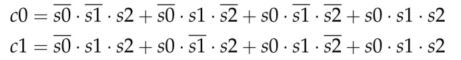
The Verilog script:

Type the following script in gvim and add them to the project.

Implement it on the Basys3 Board:

-------------------
Tasks
1. Work on the following problems: (40 points)
a. What are the fixed point representations of the following decimal numbers?
20.25 in UQ16.16
128.5 in UQ16.16
0.125 in UQ.16
-38.125 in UQ15.16
-50.0625 in UQ15.16
b. What are the floating point representations of the following decimal numbers?
0.141 in half precision/format
3.625 in half precision/format
-15.25 in half precision/format
2. Show the process of floating point addtion/subtraction of the following operations. (20 points)
a. 15.25 + 4.125
b. 15.25 - 4.125
3. Repeat the simulation work in Section 11. (20 points)
4. Repeat the work in Section 14.1, 14.2, and 14.3. (20 points)