Data types, operators, combinational logic

Relevant Digital Logic lecture videos:
Intro to number systems
Number conversion
Fractional number conversion
2's complement

The Youtube lecture playlist of Digital Logic (CE241)

1. Please review the number systems

Number conversions among binary, decimal, octal, and Hexidecimal
1's and 2's complement for negative numbers

2. Fixed-Point Representation

Binary number to be processed in a digital system may have a fractional part. There are two methods to represent a binary number with integer and fractional parts. These are fixed-and floating-point representations.

Please print and read through this PDF file for this section on the textbook.

We can show an unsigned fixed-point number (without a sign bit) as "UQp.q.", pay attention to the two dots here.
U indicates the unsigned bit notation; p represents integer, q represents the fractional part.

The Q Format or the Q Notation:

Example 1: (unsigned, UQ16.16) (U indicates Unsigned)
14.125(10) = 1110.001 (2) = 0000 0000 0000 1110.0010 0000 0000 0000
= 000E.2000
= 000E.2000 (UQ16.16)

Example 2: (signed, Q15.) (pay attention to the dot there)
-14.125(10) = 1000 0000 0000 1110 (2) = 800E (losing the fractional part)

Example 3: (signed, Q15.16)
-14.125(10) = 1000 0000 0000 1110.0010 0000 0000 0000 (2) = 800E.2000

3. Floating-Point Representation

 The IEEE 754 standard for floating point representation



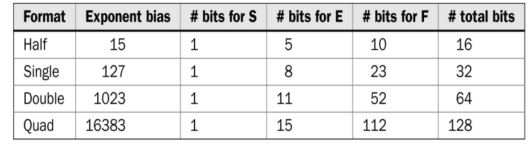
 In floating-point representation, a binary number with fractional part will be shown as N = (−1)^S × 2^E × F. Here, S stands for the sign bit, E represents the exponent value, and F stands for the fractional part. Then, floating-point number N is kept in memory as X = SEF.

Example 1:
14.125 in half precision/format:
14.125 (10) = 1110.001 = 1.110001 x 2^(3) = (-1)^0 x 2^(3) x 0.110001
=> S = 0
=> E = 15 + 3 = 18 = 10010
=> F = 110001 0000
=> X = SEF = 0 10010 110001 0000 = 0100 1011 0001 0000 = 4B10(16)

Example 2:
-14.125 in half precision/format:
X = SEF = 1 10010 110001 0000 = 1100 1011 0001 0000 = CB10(16)

Example 3:
0.125 in Half precision/format:
0.125 (10) = 0.001 (2) = 1.0 x 2^(-3)
=> S = 0
=> E = 15-3 = 12 = 01100 (must be 5 bits)
=> F = 0000000000 (must be 10 bits)
=> X = SEF = 0 01100 0000000000 = 0011 0000 0000 0000 = 3 0 0 0 (16)

You can check the results on this online conversion tool:
https://evanw.github.io/float-toy/

Verified:



Example 4:
3.141 in half precision/format:
Use an online converter to conver 3.141 to its binary form:
https://www.rapidtables.com/convert/number/decimal-to-binary.html



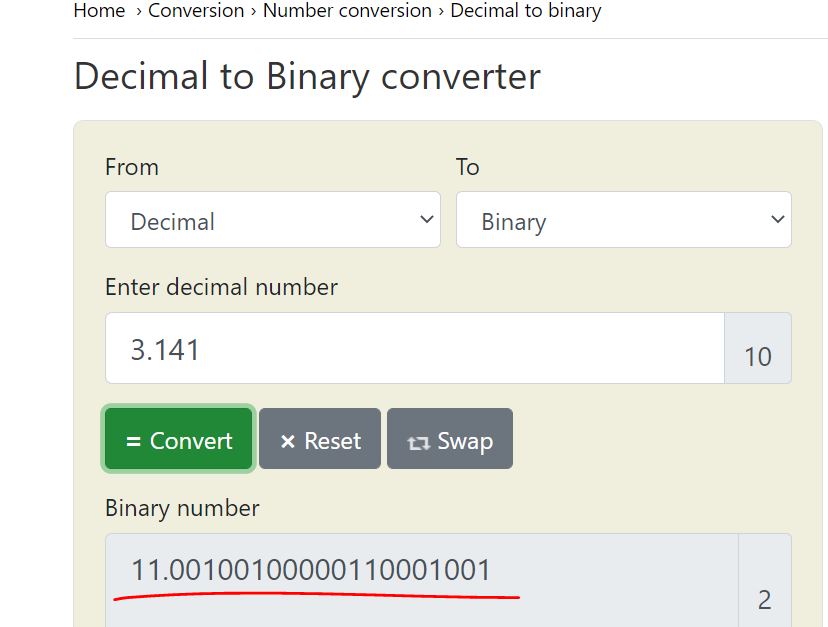
which is 1.1001 0010 0000 1100 0100 1 x 2^1
=> S = 0
=> E = 15 + 1 = 16 = 10000
=> F = 1001 0010 0000 1100 0100 1, only keep 10 bits - 1001 0010 00
=> X = SEF = 0 10000 1001 0010 00 = 0100 0010 0100 1000 = 4248

4. ASCII Code

We do not only process numbers in digital systems. For some applications, we may need to handle characters and symbols as well. We know that everything in a digital system is represented in binary form. Therefore, characters and symbols should also be represented as such. One way of representing characters and symbols in binary form is using the ASCII code. ASCII stands for the American Standard Code for Information Interchange.

To represent a specific character (or symbol), its corresponding code should be given. Let’s assume that we would like to represent the @ symbol. Using the following table, the corresponding ASCII code in hexadecimal form will be 40 (pronounced as four zero).



5. Net/Data types in Verilog

Net:
wire: a wire connecting two elements

Variable:
reg: one-bit data (a DFF)
integer: 32-bit long

Data values:
0: logic 0
1: logic 1
x: don't care
z: high impedance (open circuit or disconnected)

Constants and parameters:
examples:
1'b0: a 1-bit binary number 0
2'b10: a 2-bit binary number 10
4'b10: the binary number 0010
6'o75: 6-bit octal number (6-bit means 6 binary bits)
8'hCA: 8-bit hex number CA
8'd251: the decimal number 251 is represented by 8 bits.

Vectors:
[N-1:0] prefix: there are N net variable entries packed as a vector. MSB and LSB are the N-1th and the zeroth entries respectively.

example: wire [7:0] A. In this declaration, A is a wire data type with 8 bits. If you use 'A', it has all the 8 bits; if you use A[5:0] it only take the lower 6 bits.

example: wire [0:7] A. MSB becomes A[0], LSB becomes A[7].

A quick simulation example from the textbook:





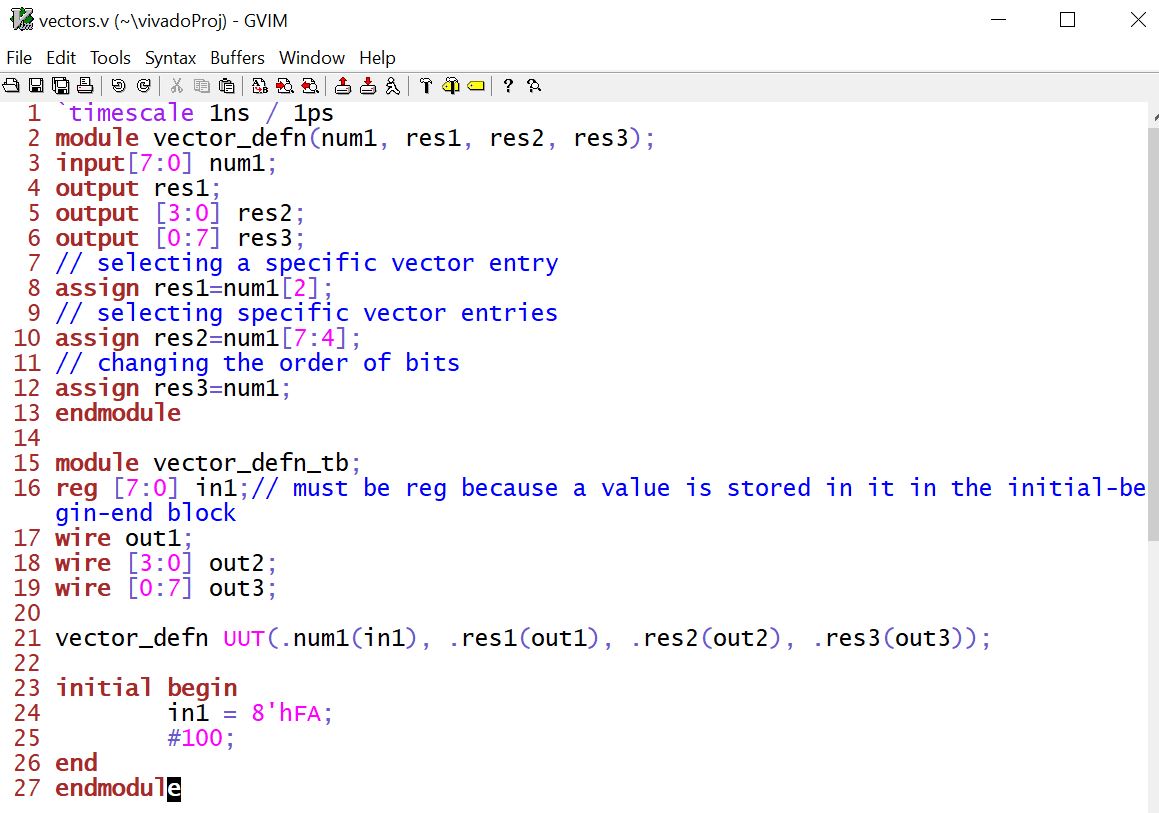
 * Logic gates

NOT, OR, AND,  XOR logic in Verilog:



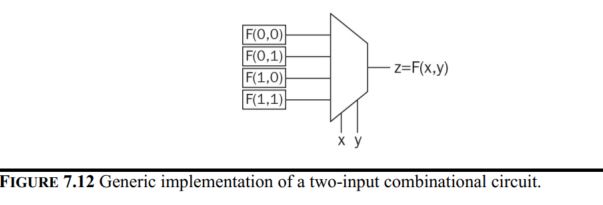
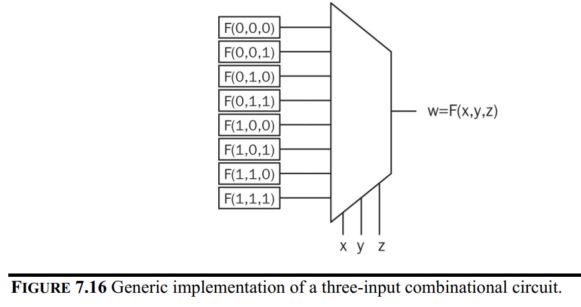
6. LUTs (look-up tables)

Combinational circuits are implemented by LUTs in an FPGA. A generic LUT is composed of a multiplexer and memory elements in its basic form. We can take the NOT gate as an example of one-input combinational circuit.



For two-input combinational circuits, the truth table and the LUT look like this:





Examples of the standard gates:



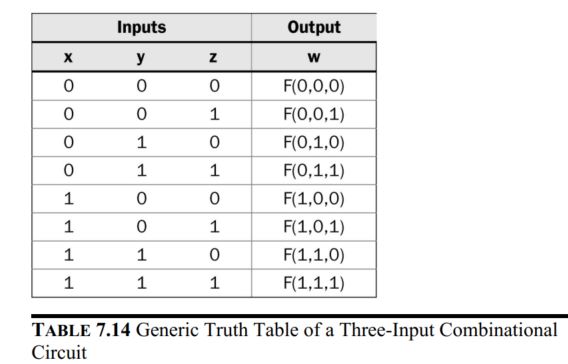
For three-input combinational circuits, the truth table and the LUT look like this:





7. Example of combinational logic design

7.1 A home alarm system


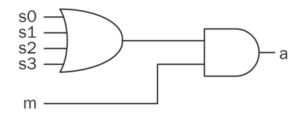
The Verilog description of the alarm system.



Implement it on the Basys3 board:

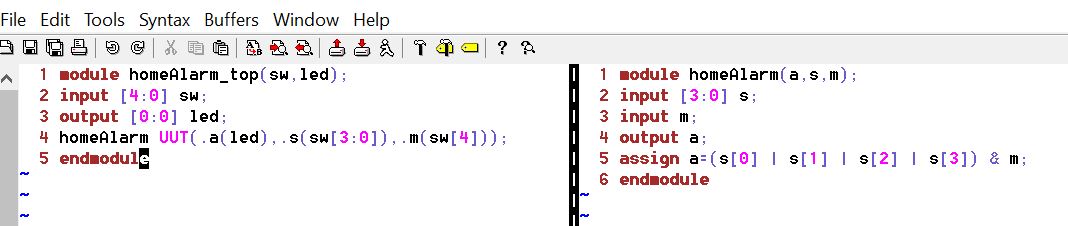
Create a new '.v' file from the command line.



Once the gvim window is opened, type the homeAlarm module into it. Also, open a new window using ':vert new homeAlarm_top.v' command.



In Vivado, disable the previous sources buy right-clicking the file and select 'Disable File'. Also, add the two source files you just created.



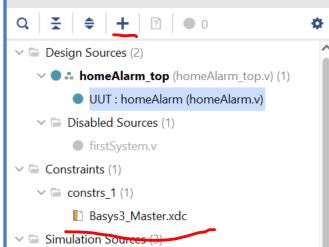
Add the constraint file 'Basys3_Master.xdc' using the '+' button. (you can download it from here. Unzip it before adding it to Vivado).



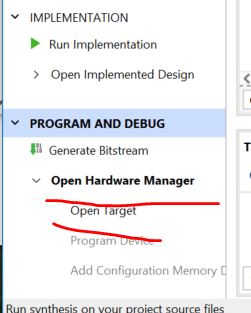
Run the Synthesis, Implementation, and Bitstream Generation respetfully.



Then click 'Open Hardware Manager' to open a new target if it is the first time to use the Basys3 Board on your computer. Otherwise, open a recent target.





Results:



7.2 Digital safe system

There is a predefined password stored in the system. Every bit of the input must match the stored bits.

Use XOR to check if every bit matches. If it does, XOR gate outputs 0's. Invert the 0's to get 1's which are used as the input to one 4-input AND gate.



The Verilog script:



Implement this on the Basys3 Board:



When the input is 0101 (MSB - LSB), led[0] lights up, otherwise, led[1] lights up.



7.3 Car parking occupied spots counting system

S0, S1, and S2 are the three spots on the parking lot. Output C1C0 is the 2-bit binary number that represents the count of the occupied spots.

The truth table of the logic:



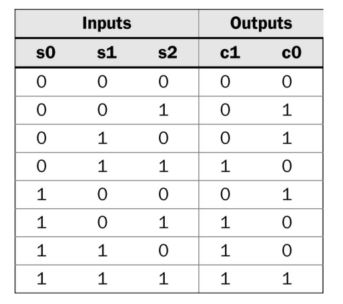
From the truth table, the following logic expression was created:



The Verilog script:



Type the following script in gvim and add them to the project.



Implement it on the Basys3 Board:



-------------------
Tasks

1. Work on the following problems: (16 points)
a. What are the fixed point representations of the following decimal numbers? Display your calculations and results in your report.
20.25 in UQ16.16
128.5 in UQ16.16
0.125 in UQ.16
-38.125 in Q15.16
-50.0625 in Q15.16

b. What are the floating point representations of the following decimal numbers? Display your calculations and results in your report.
0.141 in half precision/format
3.625 in half precision/format
-15.25 in half precision/format

2. Repeat the simulation work in Section 5. Include the snapshots of the code and simulation results in your report. (10 points)

3. Repeat all the FPGA experiments in Section 7 (Home alarm system, digital safe system, and car parking system). Include the snapshots of the code, simulation results, and FPGA demo video links in your report. (Use the ':vert new homeAlarm_top.v' command to open a new Vim window for your top module). (30 points)